¿Cómo usar machine learning para predecir la intención de compra?

​Existen algoritmos de machine learning que permiten clasificar conjuntos de datos, en lugar de predecir valores continuos. Dos de ellos son especialmente útiles en pricing: la regresión logística y los árboles de decisión. Ambos se usan cuando se desea anticipar una decisión binaria, como la compra o no compra de un producto.

Predicción de intención de compra con regresión logística
La regresión logística, al igual que la regresión lineal y las redes neuronales, se basa en grandes conjuntos de datos con variables de entrada y una variable de salida. En el contexto de precios, este tipo de regresión permite predecir la intención de compra de un cliente bajo ciertas condiciones.

Un ejemplo ilustra su utilidad. El dueño de un gimnasio sospecha que la asistencia mensual influye en la renovación de la suscripción anual. Para confirmar esto, quiere construir un modelo que le permita anticipar qué clientes renovarán, con el fin de enfocar mejor sus campañas de fidelización.

En una muestra de 20 clientes, los datos de asistencia y renovación muestran que no existe un patrón lineal claro. Como la variable de salida es binaria —renueva o no renueva—, una regresión lineal no sería apropiada.

Sin embargo, mediante una transformación matemática, es posible convertir una función lineal en una curva en forma de S, adecuada para predecir probabilidades binarias. El dueño del gimnasio usa el módulo estadístico de su hoja de cálculo para obtener los parámetros de la regresión logística.

Así descubre que quienes asisten menos de 7 veces al mes tienen una probabilidad cercana a cero de renovar. Aquellos que asisten 14 veces o más tienen casi un 100% de probabilidad de hacerlo.

Para los que están en el rango intermedio, el modelo predice una probabilidad: si es menor al 50%, se asume que no renovarán; si es igual o superior, se estima que sí.

Aunque el ejemplo usa solo una variable, la regresión logística puede incorporar muchas más, como saldos, transacciones o quejas, lo cual la hace muy útil para modelar comportamientos de compra.

Pero esta técnica también tiene limitaciones: solo funciona bien cuando la relación entre variables de entrada y salida es lineal. Cuando esto no ocurre, se requieren métodos más avanzados.

Uso de árboles de decisión para condiciones más complejas
Cuando las relaciones entre variables no son lineales, los árboles de decisión son una alternativa más poderosa. Estos también se utilizan para predecir la probabilidad de compra en contextos más complejos.

Un ejemplo lo encontramos en un concesionario donde el gerente desea estimar la probabilidad de compra de un nuevo modelo, con base en datos demográficos. Utiliza una base de datos del fabricante que contiene información sobre salario, edad, estado civil y si el cliente compró o no el vehículo.

Dado el tamaño de la base, toma una muestra de 20 registros y empieza a explorarla usando filtros. Descubre que nadie con ingresos inferiores a $2,000 compra el auto. Quienes ganan entre $2,000 y $5,000 lo compran solo si tienen más de 40 años. Y quienes ganan más de $5,000 lo compran siempre que tengan más de 40 años, o si son solteros, si tienen menos de esa edad.

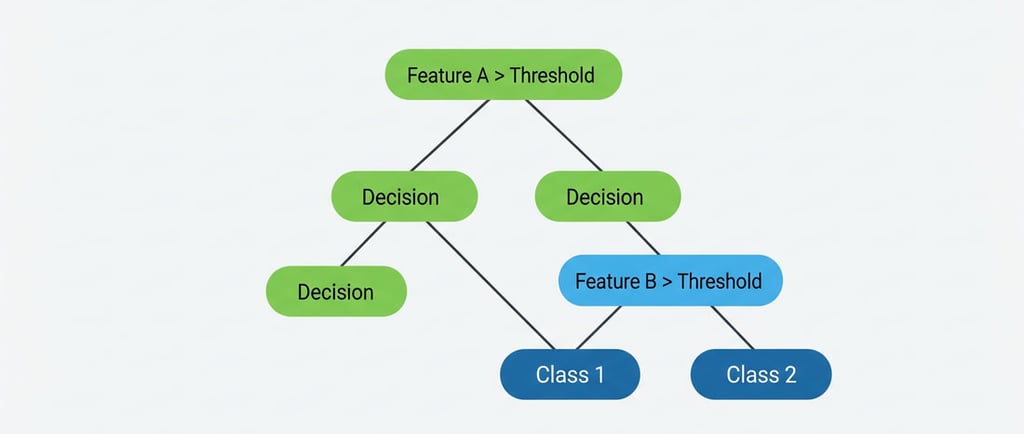
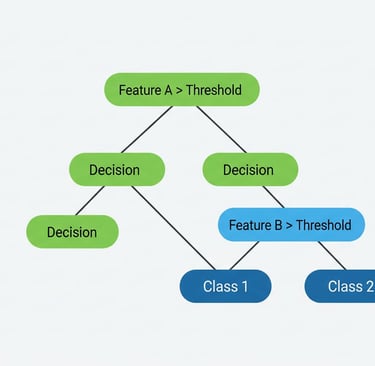
Este análisis se organiza en un árbol de decisión, donde el primer filtro (salario) es el nodo raíz, porque mejor separa el conjunto de datos. Las condiciones que siguen son nodos internos, cada uno con ramas que representan las respuestas posibles. Al final de cada camino están las hojas del árbol, que indican la predicción: sí o no.

Aunque este ejemplo se resolvió manualmente, en la práctica se requiere software especializado para identificar automáticamente las variables más relevantes y construir árboles más complejos.

Sin embargo, esta flexibilidad tiene un costo. Los árboles de decisión, al igual que las redes neuronales, pueden sufrir de sobreajuste si se hacen demasiado complejos, con muchos nodos y ramas.

Conclusión
Tanto la regresión logística como los árboles de decisión permiten predecir la intención de compra de los clientes, a partir de datos históricos y múltiples variables de entrada. La elección entre uno u otro depende de la complejidad de las relaciones entre las variables.

Hasta este punto, hemos visto modelos que requieren una variable de salida conocida. Pero ¿qué pasa cuando no la tenemos y aún así queremos segmentar a los clientes?

Eso se explora en la siguiente parte, donde se abordará el uso de machine learning para segmentar mercados sin necesidad de una variable de salida.